Student Created Review Questions

Work out these math questions.  Check in the comments section for the answers.
1.  A right triangle has legs of 15 cm and 8 cm. Find the longest side. Formula a² + b² = c²
2. Solve for x:  3x + 5 = 20, and Solve for y:  9y - 15 = 52
3. Find the surface area and volume of a rectangular prism; L= 10mm, W= 8mm, H= 7mm
4. Find the supplement of each angle. a) 65 degrees, b) 90 degrees, c) 100 degrees, d) 55 degrees
5. What is the surface area and volume for a pyramid; L= 13 in., W= 13 inches, and H= 9 inches.
Formulas for square pyramid: V=⅓ x L x W x H,  SA= (L x W) + 4 x (½ x L x slant height); 
Slant height, a² + b² = c², (½ x length)² + (height)² = c²
6. Find the volume of a cone.  Height 26 feet, Radius 15 feet, Formula for cone: ⅓ x π x r² x height
7. Find volume and surface area of cylinder. Radius 3 cm, Height 15 cm,  
Formula for cylinder V=  π x r² x height, SA = 2 x π x r² + 2 x π x r x h
8. Find the area of the similar figures.  The ratio of similar figures is 3 m = 12 cm.  The larger triangle has a base of 3 m, height 4 m. 
Formula: Area of triangle ½ x b x height.  Ratio of Similar figures is squared for area
9. Find the perimeter of the similar triangles. The ratio of similar figures is 15 inches = 3 feet.  The smaller triangle has sides of 15 in, 24 in, and 9 in.  
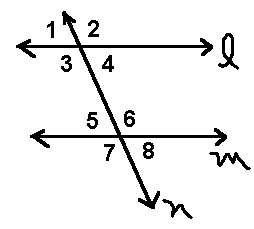
10. Find the missing angles from the picture below. Angle 1 = 75 degrees. Angle 2=___,        
 Angle 3=___, Angle 4= ___, Angle 5 = ___, Angle 6= ___, Angle 7= ____, Angle 8 =____

Which Angle Is Which?

When you hear the word angle, you probably think of right angles, acute angles, and obtuse angles, but what you may not know is that there are a lot more angles that you can find easily! 

Vertical Angle: Two angles that have are opposite each other when their two lines cross, they share the same vertex, and their sides are opposite  rays.  Vertical angles make the shape of an X. If you look at the picture above "C" and "B" are examples of vertical angles. 

Corresponding angles: Two angles that are matching each other, an example of corresponding angles are angle "G" and angle "C"

Alternate Interior Angle: When two lines are cut by a transversal, these angles are between the two lines and are on opposite sides of the transversal. Angle "C" and angle "F" are Alternate Interior angles.

Alternate Exterior Angle:  When two lines are cut by a transversal, these angles are outside of the two lines and are on opposite sides of the transversal. Angle "G" and angle "B" are alternate exterior angles.

Complementary Angles: Two angles whose measures have a sum of 90 Degrees.  The angle labeled 45° in the diagram, combined with Angle "E" which is also 45° would be complementary since their sum is 90°

Supplementary Angles: Two angles whose measures have a sum of 180 Degrees. Angle "E" and angle "F" are supplementary angles. 

You can practice finding Supplementary and Complementary Angles at AAAMath.com