A line has an angle measurement of 180 degrees. In math, supplementary angles are angles that add up to 180 degrees.
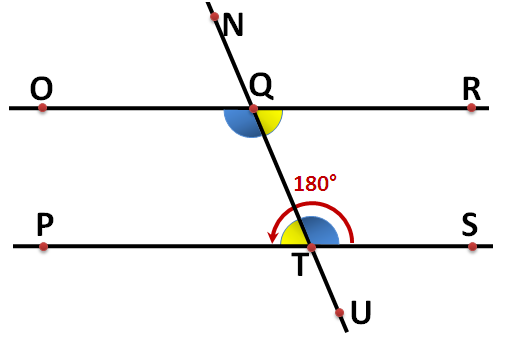
The picture to the right has us Compare Angles from two parallel lines, OQR and PTS, cut by a traversal line NQT The following vocabulary words are things we can review from this drawing.
1. Alternate interior angles are highlighted in between the parallel lines. These angles are on opposite sides and when their angle measures are combined they add up to 180 degrees. For example the yellow angles are shown to be congruent to one another in the diagram above.
2. Cooresponding angles are add up to 180 degrees and are on the same side of the traversal. the interior angle on the same side are congruent. In the diagram angle Q is congruent to the blue angles.
3. Adjacent angles are angles that are next to another and sum up to 180 degrees in the figure. Angle T and the yellow angle next to it are adjacent angles.
4. Vertical Angles are formed by the same parallel line and are not adjacent. Angle T and the blue angle across from it are vertical angles. Vertical angles do not add up to 180 degrees.
Vocabulary and Comparing Angles Practice at http://www.ixl.com/math/grade-7/transversal-of-parallel-lines
This Middle School Math Blog aims to explore math beyond the classroom into virtual space. Bloggers can find links to student blogs, math games, videos, interactive math tools, and math news/careers.
Monday, May 21, 2012
Saturday, May 12, 2012
Graphing Calculators and Problem Solving
A highlight of student work this week was using the Slope-Intercept make equations, find patterns in data, and create scatter plot graphs. It was also neat to see how students began to think of solving a system of equations using graphs of the equations:
y=.49x +10
y=.99x
Students found that the graphing calculator tool, meta-calculator.com, produced quick and accurate results.
The solution to the 2 equations above is the point where the lines intersect. This point is at approximately (20,20). So, how does this graph help answer last week's Music Download word problem?
Our definition for the variables... x= the number of songs, and the variable y= the cost of the songs.
We discovered that ...When 20 songs are purchased the price of the 2 plans happens to be the same. (around $20).
Therefore...When more than 20 songs are purchased the first plan is a better deal, when less than 20 songs are purchased the 2nd plan is cheaper.
Use the graphing calculator application to solve this problem: What solution do you find for the system of equations?
y= -3x+2
y= 2x-3
How would you check to make sure this solution is correct?
Find more interactive practice problems with answers at http://regentsprep.org/REgents/math/ALGEBRA/AE3/PracGr.htm
Friday, May 4, 2012
Slope Fits into Equations
How do we solve problems that involve changing costs, or other things that are in flux in our world? In Math equations are used to figure out all the possible scenarios that may occur. The equation y=mx+b shows a linear pattern that can be drawn on a graph or put into a table.
This week in Middle School we wanted to purchase several items that cost the same amount. The cost of each item was then multiplied by the # of items that we wanted to buy. This cost is called the slope, or the rate of each item. If we had a delivery fee, or other fixed cost that was included we had to add this to the equation too. When making a decision it is helpful to use the slope-intercept equation to explore the cost.
Here's a problem to get started thinking about how slope fits into real life problem solving...
Musicmatch, an online music store, charges a $10 dollar membership fee plus $.50 cents per song. i Tunes sells songs for $.99 cents each, but doesn't
charge a membership fee.
Which company offers a better deal for the music lover?
Set up an equation in slope intercept form
that can be used to find the cost for any number of songs.
The following website offers consumer reviews of different online music companies that may be an even better deal. Check them out at Music Download Reviews.
First we begin by comparing each music plan. In looking at the problem, What things could change as a person begins using each plan? We should be able to find two variables that can be represented by x and y in the problem.
After we have found the variables we look at the cost of each song. This unit cost, or slope is represented by the letter m in the slope-intercept equation. (y= mx+b) Slope is also called the unit cost, or rate of change. When setting up the equation we use slope to show the rate of increase or decrease. Slope is also how fast the rate increases or decreases. An interesting observation that students made while graphing lines on a coordinate plane was the steeper the line the greater the number of the slope. Can you identify what the slope is for the different music plans?
If not, or for more about the slope click on this hyperlink--- The slope.
The Y-Intercept on a graph shows where the line crosses the y-axis. In problem solving this can be also expressed as a fixed cost or starting point for how much a person would pay up front. For example, if a club has a membership fee that must be paid in addition to buying songs. For example, if i tunes had charged a $5.00 membership fee this would be added on to the equation. y=.99x + 5 Can you tell what the y-intercept for Musicmatch would be? Does i Tunes have a Y-intercept, why or why not?
The slope and y-intercept are written in Slope Intercept Form. (y=mx+b) As we try different values and put them in for the x=#of songs, or y=total cost, we can further explore the advantages of each music plan.
Which plan did you find to be the better deal for the music lover? What other strategies can use to solve this problem?
I found it interesting to explore music plans that are available online. It would be great to hear about other plans that are advantageous, or other links that would give data to support this inquiry.
This week in Middle School we wanted to purchase several items that cost the same amount. The cost of each item was then multiplied by the # of items that we wanted to buy. This cost is called the slope, or the rate of each item. If we had a delivery fee, or other fixed cost that was included we had to add this to the equation too. When making a decision it is helpful to use the slope-intercept equation to explore the cost.
Here's a problem to get started thinking about how slope fits into real life problem solving...
Musicmatch, an online music store, charges a $10 dollar membership fee plus $.50 cents per song. i Tunes sells songs for $.99 cents each, but doesn't
charge a membership fee.
Which company offers a better deal for the music lover?
Set up an equation in slope intercept form
that can be used to find the cost for any number of songs.
The following website offers consumer reviews of different online music companies that may be an even better deal. Check them out at Music Download Reviews.
First we begin by comparing each music plan. In looking at the problem, What things could change as a person begins using each plan? We should be able to find two variables that can be represented by x and y in the problem.
After we have found the variables we look at the cost of each song. This unit cost, or slope is represented by the letter m in the slope-intercept equation. (y= mx+b) Slope is also called the unit cost, or rate of change. When setting up the equation we use slope to show the rate of increase or decrease. Slope is also how fast the rate increases or decreases. An interesting observation that students made while graphing lines on a coordinate plane was the steeper the line the greater the number of the slope. Can you identify what the slope is for the different music plans?
If not, or for more about the slope click on this hyperlink--- The slope.
The Y-Intercept on a graph shows where the line crosses the y-axis. In problem solving this can be also expressed as a fixed cost or starting point for how much a person would pay up front. For example, if a club has a membership fee that must be paid in addition to buying songs. For example, if i tunes had charged a $5.00 membership fee this would be added on to the equation. y=.99x + 5 Can you tell what the y-intercept for Musicmatch would be? Does i Tunes have a Y-intercept, why or why not?
The slope and y-intercept are written in Slope Intercept Form. (y=mx+b) As we try different values and put them in for the x=#of songs, or y=total cost, we can further explore the advantages of each music plan.
Which plan did you find to be the better deal for the music lover? What other strategies can use to solve this problem?
I found it interesting to explore music plans that are available online. It would be great to hear about other plans that are advantageous, or other links that would give data to support this inquiry.
Wednesday, May 2, 2012
Aladdin Jr and Algebra Word Problems
Swift School is putting on a musical performance entitled, "Aladdin Jr" next week, and we are expecting many children and adults to attend. The ticket counters at the play will surely be wondering how many adults and children attended Aladdin Jr. I found a similar question about "Theater tickets" that a student posted on http://www.algebra.com/
Try reading the question and solving it on your own before reading through the solution. Check your answer with the one shown below.
What other strategies do you know to solve this problem?
Try reading the question and solving it on your own before reading through the solution. Check your answer with the one shown below.
What other strategies do you know to solve this problem?
Subscribe to:
Comments (Atom)