About Me...By the Numbers

About me...By the Numbers is a project that uses numbers to show a picture about You.
So, Which numbers have special meaning for you?
The picture above shows an example project from Pinterest.
Directions: 1.  Write your name in the center of the paper.  2.  Brainstorm facts about you that involve numbers.  For example my dad had 16 siblings, my birthday is 6/27, and I my baby daughter weighed 6 pounds 11 ounces when she was born.  3. Write 5 or more numbers about yourself in the area outside your name.  4. Decorate and add a short description about the meaning of the numbers.

Numbers important to me....
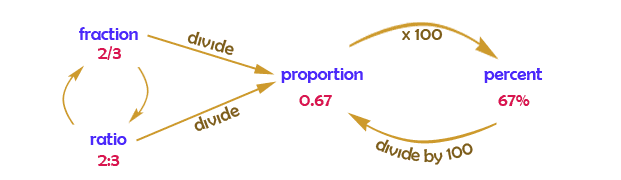
 Fractions:  Birth date, favorite holiday, # of ____ in family / total family members.
Large Numbers: distance from my house to a relative's house, number of days until Christmas Break, height in centimeters
Decimals: cost of favorite candy  $0.25, distance of a 5 kilometer race= 3.1 miles, weight of a baby 7.2 pounds

Keeping a Writer's Notebook

"As a writer, words are your paint. Use all the colors.” ~Rhys Alexander. 

 Being a writer is very much like being an artist.  I wanted to share my seed story starters, summer math problems, and resonating writing ideas.  I look forward to crafting new stories, solving math problems, and sharing things I've learned.    

Summer moments make for great seeds for a Notebook of ideas.

• "After a hot evening on the field, a team that is down by one run comes up to bat"
• "A girl sings to the movie as her favorite song begins to play"
• "The alarm sounds at 5:30am, as my feet hit the floor I prepare for the big day"

Here are some great examples of writing notebook ideas from an inspiring writer/teacher on Jordan's blog page: Writing Notebook Ideas 

Math problems are very rewarding after figuring out the solutions and then telling how you found the answer.

• Summer programs include instrumental music, art, and dance.  Out of 40 students, 15% chose art. How many students are signed up for art? how many signed up for music or dance?
• A bedroom is 8 feet tall, 12 feet wide, and 9 feet long.  How many square feet of paint are needed to paint the 4 walls and ceiling?

Ready for more?  Try 16 fun math problems from a website called, Analyze Math: Math Word Problems

Summer Writing Ideas to Begin With...

1. Types of writing to try:  Compare and Contrast two of your favorite comics, books, or magazines.
2. Write a story about one of the characters from a book you are reading. 
3. A story about a loved one and how they have made a difference in your life. 
4. Which type of (phone) do you prefer; (iPhone or Android)?
5. Research and then explain about a (country) that you have always wanted to know more about. 

Always love to hear YOUR comments:) 

Summer Math Fun

Where can you find math in your life?  What ways do you like to do math?   Summer math activities are fun and will definitely sharpen your mind.  Which of the ideas below work best for you?   You probably have already tried many of these, so feel free to leave comments about math activities you enjoy.

Playing Card or Dice Games  

Multiplication- Each player draws two cards and multiplies the numbers.  The player with the higher product wins.  Challenge: Use 2 digit numbers or decimals by drawing four cards instead of two.

• Times table fact practice
• Decimal Multiplication

Fractions- Each player draws four cards and arrange in any order.  Add the fractions, the player with the greater sum wins.  Challenge: Use mixed numbers by drawing six cards instead of four.

• Fraction Number Lines
• Fraction Bars   

Art Projects

Draw a scene that has hidden geometric shapes.  Use both basic shapes and more complex shapes in the drawing. Challenge:  Create a fractal design

• Sierpinski Triangle Design
• Use Symmetry to Create Logos

Computer Games

Play math games that others created or try your hand at coding and make your own game.  Some games allow you to compete against others, whereas others let you try to simply master the game itself. 

• Manahigh.com 3-D Math Games
• Matholpolis- Improve your mental power

Ratio Projects

Darlene and Jackie decide to share the profits from the latest business venture 5:3.  If Jackie receives $210.00 how much money can Darlene expect?

At the spring festival there are 22 attractions that are split between food and entertainment.  Out of these attractions 6 are food stations.  What percent of the attractions have food?  

Lucy spent 54 Euros on a new pair of gym shoes including tax.  If tax was 10 percent, what was the cost of Lucy's shoes before tax?  

Answers:  

1. $350 dollars for Darlene.  210*5=1050  

1050/3 = 350

2.  27% were food stations  6/22= .272

.273*100 = 27.3%  

3. 49 Euros before tax.   54=1.10x    54/1.10= 49.09

Graphing Equations and Inequalities. Which do you prefer?

What types of graphs do you like to create? One of my favorite parts of Math is graphing and finding patterns in problems.  Graphs and Charts are found in many parts of our every day life.  

Pie graphs and bar graphs that are used to compare things like people's opinions for example.  Line Graphs and scatter plots are a type of graph that shows the relationship between two quantities or show can show changes over time.  The pattern on a line graph shows an increase (line goes upward) or a decrease (line goes downward).  

How do I graph an equation?

1. Equations such as y = 2x + 3 can be graphed by making a table of values for both x and y variables.

X	Y
-1	1
0	3
1	5
2	7

Steps to make a table of ordered pairs

a. Choose values for x that include both positive and negative numbers.
b. Substitute the value for x into the equation.
c. Use order of operations to solve the equation and find a value for y.
     Example   x = -1   y = 2x  + 3
                                  y = 2(-1) + 3   Substitute -1 for x
                                  y = -2 + 3       Then multiply 1 * -2
                                  y = 1               Add -2 + 3
2.  Use a coordinate grid to plot the ordered pairs in the table.
Example:  Ordered pairs:  (-1,1), (0,3), (1,5), and (2, 7)

The solid green line shows the pattern of the equation.  It is increasing or going upwards.
Y- Intercept-  The point where the line crosses the                   y-axis.  The green line crosses at (0,3)
Slope-  The slope of the line is how steep the line rises in the graph.  Find the slope in the equation:
Y=2x + 3.  The number that is multiplied by x is the slope. The slope of the green line is 2.





How do I graph an Inequality?

Inequalities have an inequality symbol like <, >, ,≥, or ≤  instead of an equal (=) sign.
1. Inequalities like y ≤  2x +3 are graphed by making a table of values, the same as we did when there was an equal sign.
2.  The points are plotted on a coordinate plane in the same way that the equation y = 2x +3 was done.
3.  Here's the difference, the line that you draw to show the pattern of the points will be solid since the it is ≤  (less than or equal to), and you will color in underneath the line to show all the possible solutions to the inequality y ≤  2x +3.

The purple shaded area shows all the possible solutions of  y ≤  2x +3
The solid blue line shows that the inequality sign is ≤ less than or equal to.  The line is solid since the solution set also includes all the ordered pairs in the equation y = 2x + 3
The slope and y-intercept are the same as the y = 2x + 3 graph.




When the inequality is greater than, the purple shading will be above the line like the image below.

The equation for the image below would be y > 2/3x - 2.  The blue line is dotted because the
    > (greater than) symbol does not have a line underneath it.  It is only greater than and not equal to.

The dotted blue line shows that the inequality does not include the solution set y = 2/3x - 2.
The slope is 2/3 because the equation the graph shows that the line is going upwards; the rise is 2 and the run is 3.
Slope is rise ÷ run
The y-intercept is -2 because the blue line crosses the y-axis at -2.

How do I use a graphing calculator to Graph equations or inequalities?  Which of the graphing calculators do you like best?

1.  Go to a free graphing calculator website like Desmos, Meta-Calculator, or NCES Create A Graph.

2.  Write the equation or inequality into the website.  Then, click the "Graph" option.

3.   Many websites allow you to print the graph, or even save it as a picture.

To sum it up, graphing equations and inequalities on computers can be an efficient way to create your graph.  The graphs can then be used to compare data and help you think about the information in new ways.  

Here some equations to graph.  What do you notice about the graphs?  Do the pairs of equations have any common solutions? 

First pair of equations

y= 5x 

y=2x + 3

Second pair of equations

y=3x + 4

y=3x - 2

Inequalities
y > 2x + 3

y > x^2

Tri-Fold Booklet

Scoring Rubric:
Math explanation-  Uses accurate math terminology, steps of what was done to solve the problem, explains why each step was done, completely explains how I found my answer.
Strategy- Includes pictures, lists, charts, or symbols to shows solution for the problem.  Shows how the parts of solving the problem relate to each other, shows more than one approach to solving the problem.
Accuracy-  Clear math thinking and accurate calculations, math concepts are well developed, labels are used accurately.

Foldable steps: 
1. Fold an 8 1/2 by 11 piece of paper in half the long way
2. Hold the long way and fold it in thirds by making two folds 3 3/4 inches from the sides
3. Cut down the two folds to fold in the center of the paper.
4. Fold the three flaps down
5. Fold the two side flaps on to the center panel.

Valentine's Day Project

What is your favorite type of candy for Valentine's Day?
Candy comes in many different packages, and often has a variety of kinds.   For example, a typical box of chocolates has fruit, cream, and nut fillings.  The different types of chocolate can be quantified using these categories.

Type    Quantity    Fraction
Fruit     6                6/22

Cream   4              4/22

Nuts   12               12/22

Total      22            22/22


Each of type can be described as a part of the whole box.  In the chart above the amount of candies that have either fruit or cream filling would be 10/22 or 5/11 of the chocolates.

If a candy company decided that it wanted to increase the amount of fruit and creams so it was 8/11 to satisfy its customers what would be the number of nuts filled candies in the box?

Poster Problems

A rectangular field is 30 feet long and 20 feet wide.
There are 4 evenly sized sections to the field, what is the area of each section?
What are other possible ways the field could be divided into evenly sized sections?

A Super Bowl drawing has prime numbers as winners. What is the probability of a getting a prime number if the numbers included are 2-29?  Would the probability be greater or less if it was numbers 2-10?

World's Fair Math Explanation Example

Surface Area and Volume of a Building

The Harold Washington Library is in the shape of a rectangular prism for the main building.  I want to find the surface area and volume of the building.  The surface area of is the total area of all the faces.  Surface area is measured in square units (cm²) because like area it is the amount of material that covers a flat surface and can be put into square units of measure.  The other measurement that I want to show is the volume which is the space inside the figure.  Volume is measured in cubic units (cm³) because it is measuring the units inside of a 3 dimensional figure. 

The HWL is approximately 50 feet long, 25 feet wide and 30 feet tall.

Surface area = Sum of all 6 of the rectangular faces 

SA= 2 (lxw) + 2 (lxh) +2 (wxh)

SA= 2 (50x25) + 2 (50x30) + 2(25x30)

SA = 2 (1,250) + 2 (1500) + 2 (750)

SA = 2,500 + 3000 + 1500

SA = 5,500 + 1500

Surface Area = 7,000 square feet  

I found the surface area of the rectangular prism by measuring the area of the 6 faces of the prism.  I knew there were 6 faces from the net drawing of a rectangular prism.  First I knew the building was 50 ft. length, 25 ft. width, and 30 ft. height and put them into the equation.  SA= 2 (lxw) + 2(lxh) + 2(wxh). I multiplied inside parentheses first.  For example, 50x25=1,250. Then I knew that the 2 on the outside meant to multiply since there was a number next to a parentheses.   So I multiplied 2 times 1,250 to get 2,500 using mental math. I multiplied by two because I knew the top and the bottom of the prism were the same size. The front and back sides were each 750 square feet, or 25 times 30, and the top and bottom were each 1,250 which was found by multiplying 50 by 25.  Then I doubled the front to find the total area of the front and back sides since they were both 25 by 30. 1500 times 2 equaled 3,000.  The combined surface area was found by adding all these areas together 2,500 + 3,000 + 1,500 was 7,000 square feet.  I checked my answer using a calculator and found the surface area of the rectangular prism would be 7,000 square feet.

Volume of a rectangular prism= Length x Width x Height

Volume = 50 x 25 x 30 =  37,500 cubic feet

The volume of the figure was found by using an equation.  I knew that the base of the figure was 50 by 25 feet.   So, I multiplied 50 times 25 to get 1,250 square feet.  The height of the rectangular prism was 30 feet, so I multiplied the base times the height to find out how much volume spans up the height of the prism.  I found that 1,250 times 30 was 37,500 cubic feet.  The volume of the rectangular prism is 37,500 cubic feet.  

Reading Projects

Create a culminating project about the novel that you have read.  In your project write about the themes and main topics that were addressed.  Include the vocabulary terms that you learned, character analysis, and conflict/resolutions.

Format: PowerPoint Presentation, Poster Board, or Book Blog.
Grouping Preference: Group vs. Individual Projects
Due Date: December 10th

• Group Projects or Individual Projects:  Group projects should include multiple aspects of the book, the projects should describe more chapters, or aspects of the book (tone of the book, questions/answers, polls, and other features that you learned from your book)  
• Individual projects should be focused on a central theme or topic of the book.  The individual project can include some information about a favorite chapter or specific aspect of the book.  (tone, questions/answers, polls and other features)

Triangle Properties

Angles

What is the sum of the interior angles of any triangle?
If angles 1 and 2 are 40 degrees and 60 degrees what is the missing interior angle? What is the measure of the exterior angle?

Sides

What is the relationship between the sides of any triangle?   If side a is 8 centimeters, what is the length of sides b and c?  When we add two sides of the triangle how does the sum compare to the remaining side?

Tax Problems

Janice went to Jewel Food Store and bought a box of Orange Popsicle for $3.30.  The tax rate for groceries was 4%. How much would 4 boxes of Orange Popsicles cost? (Include tax)

Step 1:  $3.30 X 4 boxes = $13.20

Step 2: $13.20 X 1.04 (4% tax) = 13.728      (1.04  = 1 + .04   (1 to get the cost, and .04 for 4/100 tax)

The total with tax would be $13.73 (Rounded to the nearest cent)

Assignment: Write your own tax problem.  Include the cost of the product.  Find out how much the item would cost after a 4% tax is included.                       

Riddles and Limericks

What riddles do you know?   Halloween riddles from kidspot.com.au

A. What's a ghost's favorite dessert?  

B. What movie do ghosts love to watch?

C. What did the boy ghost say to the girl ghost?

D. What kind of roads do ghosts haunt?

E. What did the polite ghost say to her son?

F. Who was the most famous French skeleton?

And a Limerick...  From briandehumor.com
          Mosquitoes

Mosquitoes are what a bat eats,

For him they are edible treats,

He's known to devour,

A thousand an hour, 

We're happy when he overeats. 

A limerick is... a 5 line poem.  It has rhyme pattern on Lines 1, 2, + 5, Lines 3+4.  The limerick has 36 syllables- 8 each on lines 1,2, + 5, and 6 each on 3+4.  The last line usually has a punch line, or play on words.  

Write a limerick  

1. Start by brainstorming a funny/silly idea. (make a question, + answer it)

2. Write lines 1 and 2 end with a rhyming word.  (Need help with rhymes try- rhymezone.com) 

3. Add lines 3 and 4 (just 6 syllables each)

4. Finish with your punchline. (answer to question)

        

     Freedom (No Turning Back)                

                         by, Mr. Hull  

     Fresh air rushes into my lungs,
     New life appears like a bell rung.
     My old burdens escape,
     Tears spill free from my face.
     Hope grows for a new life begun.  

Riddle Answers  A. I-scream  B. High S-ghoul Musical  C. You look boo-tiful tonight

D. Dead Ends  E. Don't spook until your spooken to   F. Napoleon Bone-A Part 

Book Club Discussions

Book Club Discussion Starters

Who are the main characters in the story, what challenges do they face?

Describe the setting or background of the story.  (Time period, cultures, family structure)

What is the tone of the story so far?  (Does it feel tense, exciting, sad?  Support with examples)

Mystery Number Questions

Create a mystery number problem using integers.   Use these ideas for developing your clues.  Begin by picking a number between -100 and 100

• Odd or even?
• Is it a positive or negative number?
• Is it a square number
• Can you name some of the factors?
• More or less than a number?

Here's an example....

I'm thinking of a number that is less than -10

It is an even number

The number is a multiple of 4 and 9

When you add the absolute value of the digits together you get 9.

Summer Training Plans

How do you get ready for an upcoming bike ride, walk, or run?  The Training Plan below is a way to help people prepare for a big event.  This plan also be used for finishing a book, writing a story, or a big project.

The training plan uses something called The 10 Percent Rule.  This rules says you should increase your current activity level by 10 percent per week so that you don't over train (during running)

For example, if you were wanting to do a 20 mile run by the end of the summer, and currently you are running around 10 miles per week, would this be possible? Let's say that the end of the summer was 7 weeks away.  First, you might prepare by making a Table of how many miles you'll be running each week.

Table

Weeks    Equation     Miles Ran  
1            10*1.1              11    
2            11*1.1            12.1
3           12.1*1.1          13.3
4           13.3*1.1          14.63
5           14.63*1.1      16.093
6          16.093*1.1       17.7
7          17.7*1.1           19.47
x           10*1.1^x      

In the table you can see that each week you increase the Miles Ran by 10%.  The equation uses 10% written as a decimal 0.10.  Beginning with week 1 you find what is 10% more than 10 miles?  A shortcut in using percents, when multiplying by 1 you get the same number so instead of multiplying times 0.10 we can switch it to 1 + 0.10 or 1.10.
The equation column shows 10*1.10= 11, So in week 1 you plan to run 11 miles.  Then, in week 2 you start with 11 and find out what 10% more is by doing 11*1.10=12.1 miles. When doing the math you probably noticed that you multiply the total for the week by 1.10. You could keep going with this pattern through week 7 to find the total number of miles by week 7.

Another strategy you may have already thought of is Using an Equation involving exponents. The exponents can help you find out if it is possible to reach the goal by a certain number of weeks. Let's say 6 weeks?
Since you are using an equation you use the starting distance which was 10 miles and the percent increase 1.10,  the number of weeks is the exponent function in the equation. Starting distance times  1.1 ^ x weeks
10 miles*1.1^6 weeks =  17.712 miles. (Notice this is close to the value in the table, but not exactly)
10 miles*1.1^7 weeks= 19.47 miles
After 7 weeks you are still slightly less than the 20 mile goal at 19.47 miles. However, if you round up to the nearest tenth of a mile, you're at 19.5 miles.  You could Check your Answer by filling in the other values in the table above.

This plan of increasing by a percentage each week can be used for other projects. Right now you're writing 3.5 pages a week, but want to finish a young author's project that is going to be 25 pages long in 4 weeks.  If you increase your rate by 10% each week, will you finish by the deadline?
 Week              Pages per week
Starting                    3.5
1          3.5*1.1      3.85
2         3.85*1.1     4.235
3         4.235*1.1   4.6585
4        4.6585*1.1  5.124
Total Pages written  21.4 pages written

Want to learn more about How Percents Work check out this video and other fun activities
on Brain Pop.com Interest % Movie

End of School Year Projects and Weblinks

Display Boards 

Middle School Hero's Projects

Hero Day Celebration

Class of 2013 Career Day Trip

The month of June has been full of celebrations!  Students used technical drawing & coordinate geometry to create a portrait of their Heros.  We used the coordinate grid to draw an identical image of the hero.  Students shared their projects on our Hero's Day celebration.  

Another celebration was a Career Day Field Trip.  This trip was made possible by Gear Up Chicago.  Students won prizes for team building activities and learned about careers.

Weblinks:

Mr. Martini's Classroom-  Online practice with long division and equations.  Allows you to keep track of your score.  You can also learn step by step long division without using paper and pencil.  

Extreme Math- A 3-D game with Rock Music.  Watch the "Extreme" character perform ski tricks when you get the answers right.  

Mathopolis-  Math Contests with kids from all over the Globe. Earn merits for games won, and correct answers.  

How do you find the side length of a square when you know the area?   Area of a square is side times side.  For example if the area is 25 cm² and 5 x 5 = 25, the side length = 5 cm. 

Square roots are found using the perfect squares.

1² = 1            √1 = 1           Square root of 1 = 1

2² = 4            √4 = 2           Square root of 4 = 2
3² = 9            √9 = 3           Square root of 9 = 3
4² = 16         √16 =4           Square root of 16 = 4

Can you find the square roots for 25, 36, 49, 81, 100, 121, and 144?  What patterns do you notice?

Try the Square Root Game on SoftSchools.com

Interest Earned by Saving and Investing

    

Exponential Growth-  change that happens when a beginning amount grows by a consistent rate over time.

Develop a Savings or Investment Plan

      1. Make a goal for saving or investing money.  

2.   Decide on a beginning amount to put toward your savings or investment goal.

3. Choose an interest rate.  Savings account (.005-.01),  Investment Account (.01-.09)

Website Links: Savings interest rates

                        Investing interest rates

4.  Construct a table to record your data.  Include beginning amount, interest earned, and ending amount

5.   Create a line graph to show changes over time. 

Example Savings Goal

Goal- $2,000 down payment on a used Toyota Prius in 5 years

Beginning Amount $800.00

Interest Rate: 6% (.06)  Mid-Term Bond Mutual Fund

Year       Beginning       Yearly        Interest       Ending 

                 Amount        Savings     Earned         Amount

1              800                 100                 54                      954

2              954                 100                 63                     1117

3              1117               100                 73                      1290

4              1290               100                 83                      1473

5              1473               100                 94                      1667

6    6              1667               100                106                     1882

      7              1882               100                119                     2101

Student Created Review Questions

Work out these math questions.  Check in the comments section for the answers.
1.  A right triangle has legs of 15 cm and 8 cm. Find the longest side. Formula a² + b² = c²
2. Solve for x:  3x + 5 = 20, and Solve for y:  9y - 15 = 52
3. Find the surface area and volume of a rectangular prism; L= 10mm, W= 8mm, H= 7mm
4. Find the supplement of each angle. a) 65 degrees, b) 90 degrees, c) 100 degrees, d) 55 degrees
5. What is the surface area and volume for a pyramid; L= 13 in., W= 13 inches, and H= 9 inches.
Formulas for square pyramid: V=⅓ x L x W x H,  SA= (L x W) + 4 x (½ x L x slant height); 
Slant height, a² + b² = c², (½ x length)² + (height)² = c²
6. Find the volume of a cone.  Height 26 feet, Radius 15 feet, Formula for cone: ⅓ x π x r² x height
7. Find volume and surface area of cylinder. Radius 3 cm, Height 15 cm,  
Formula for cylinder V=  π x r² x height, SA = 2 x π x r² + 2 x π x r x h
8. Find the area of the similar figures.  The ratio of similar figures is 3 m = 12 cm.  The larger triangle has a base of 3 m, height 4 m. 
Formula: Area of triangle ½ x b x height.  Ratio of Similar figures is squared for area
9. Find the perimeter of the similar triangles. The ratio of similar figures is 15 inches = 3 feet.  The smaller triangle has sides of 15 in, 24 in, and 9 in.  
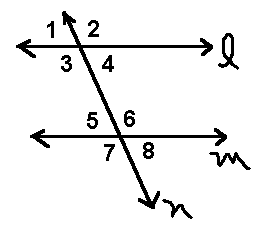
10. Find the missing angles from the picture below. Angle 1 = 75 degrees. Angle 2=___,        
 Angle 3=___, Angle 4= ___, Angle 5 = ___, Angle 6= ___, Angle 7= ____, Angle 8 =____